Определяем меру риска (VAR) в Excel
 7 мин
7 мин
 12333
12333  5 Май 2020
5 Май 2020 
Основатель и Генеральный директор, SF Education

Инвестору чрезвычайно важно знать степень риска, которому подвержены открытые позиции. Определить меру риска VaR (Value-at-Risk) для единичного актива можно по формуле:
95% VaR = 1.65 X Волатильность * Размер позиции * SQRT(Время)
где
(SQRT – корень квардатный) и 95% – это 95%-ный доверительный уровень;
Волатильность – стандартное отклонение изменения цен (выясняется как натуральный логарифм «сегодня/вчера»);
Размер позиции – лицевая стоимость торгуемого контракта;
Время – горизонт оценки.
Полученный результат трактуют так: ценовые изменения в данный промежуток времени не приведут к потерям выше полученного результата в 95% случаев. Иными словами, есть только 5%-ная вероятность потери, превышающей значение 95% VaR.
В банковской практике чаще применяется 99% VaR, отличие которого от представленной формулы в коэффициенте: 2.33 вместо 1.65. Соответственно, 99% VaR говорит нам, что цены с вероятностью 99% не способны измениться настолько, чтобы убытки превысили вычисленное значение.
Пользуясь указанной выше формулой, можно определить риск широкого спектра финансовых активов, попадающих в категорию простых инструментов и линейных производных. К ним относятся: акции, иностранные валюты, облигации обычные и с плавающим купоном (не имеющие высокую дюрацию), процентные и валютные свопы, валютные форвардные контракты, FRA. Тем самым формулировка доступна для применения практически на всех рынках, традиционно вызывающих интерес у отечественных инвесторов, в первую очередь – на рынке акций и FOREX.
Обычно проблемы оценки риска рассматриваются на стадии портфеля, состоящего из двух активов. Для большего числа инструментов предлагаются формулы, труднопонимаемые без специальной математической подготовки. Но данная задача решается просто, если подойти к ней сугубо с практической точки зрения, исключив теоретические аспекты.
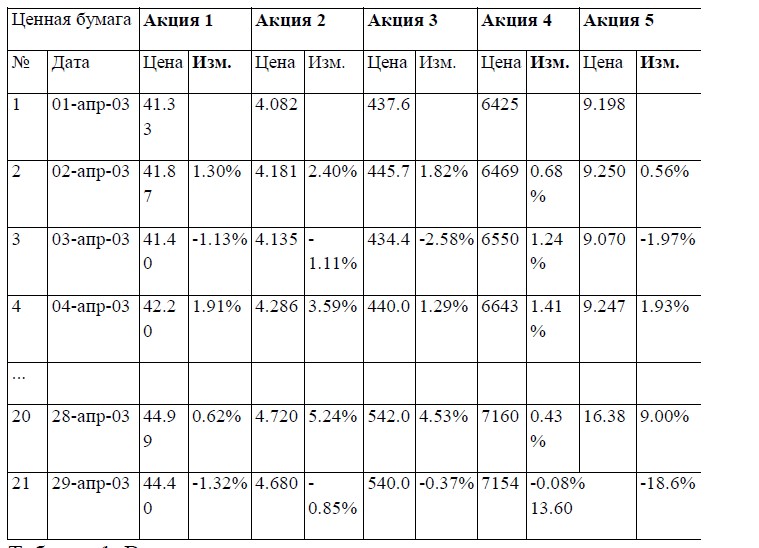
Поэтому здесь дается только то, что необходимо знать, чтобы самостоятельно составить программу в электронных таблицах (Excel), обеспечивающую вычисления VaR портфеля. Для иллюстрации использованы случайно выбранные пять российских акций в произвольно взятый период времени: с 1 по 29 апреля 2003 года.
Шаг 1. Первичная обработка данных
Сначала выясним значение среднего изменения цен и волатильности. Для этого нам потребуется как минимум объем данных, удовлетворяющих выбранному периоду оценки.
Предположим, используется 20-периодный цикл, тогда нужно не менее 21 дня, если анализ выполняется по дневным данным. Для каждого дня необходимо выяснить натуральный логарифм отношения цен «сегодня/вчера» (см. значение «Изм.» в табл. 1).
«Изменение» = ln (сегодня / вчера)
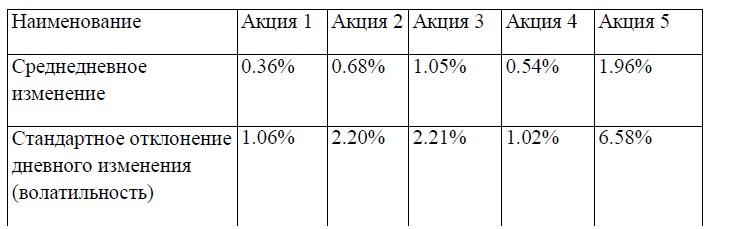
Теперь можно найти среднедневное изменение и величину стандартного отклонения, используя полученный ряд (колонки «Изм.»).
Среднедневное изменение – это среднеарифметическое, которое в Excel записывается «=average()», а стандартное отклонение как «=stdev()», которое и является дневной волатильностью.
При этом калькуляция охватывает область переменных, находящихся на строчках от 2 до 21 в колонке «Изм.» (результат см. в табл. 2).
Следует иметь в виду: предлагаемый алгоритм оценки волатильности основан на методе постоянных, а не экспоненциально взвешенных ковариаций. Но к ним можно перейти, используя полученные ряды изменения цен, для чего необходимо ввести соответствующие поправки, обеспечивающие больший вклад более поздних наблюдений.
Хороший аналог данного метода оценки волатильности – взвешенная скользящая средняя по сравнению с обычной скользящей средней. Характерно, что множитель, практикуемый в методологии J.P. Morgan RiskMetrics, равен 0.98, как и в установках по умолчанию в программах, предназначенных для технического анализа рынка.
Шаг 2. Необходимый минимум теории
Прежде чем перейти к вычислению VaR портфеля, обратимся к некоторым сведениям, которые дают понимание расчетных алгоритмов. В целом VaR портфеля из многих активов можно определить по следующей формуле:
VaR портфеля = Среднее изменение – К * Волатильность портфеля,
где
Среднее изменение – просто сумма средних изменений всех компонентов портфеля;
К – число стандартных отклонений, требуемых для заданного доверительного уровня, вычисляемое по формуле в Excel «=NORMSINV()», где аргумент – соответствующий доверительный уровень.
Волатильность портфеля калькулируется с использованием формулы, предложенной Г. Марковицем:
Волатильность портфеля = SQRT (Вектор волатильной компоненты *Корреляционная матрица * Транспонированный вектор волатильной компоненты)
Вектор волатильной компоненты можно вычислить, пользуясь формулой:
Компонента волатильности = Стоимость позиции * Волатильность позиции
Помимо уже выполненных расчетов для вычисления VaR портфеля потребуется построить корреляционную матрицу, основываясь на данных, обработанных в шаге 1.
Она представляет собой совокупность коэффициентов, отражающих корреляцию между каждым из инструментов, входящих в портфель.
Вычисления в Excel выполняются с помощью соответствующей функции «=correl()», причем построение матрицы лучше выполнить на странице, где будут размещены все прочие расчеты, в том числе и VaR. Это уже будет шаг 3.
Шаг 3. Вычисление VaR портфеля
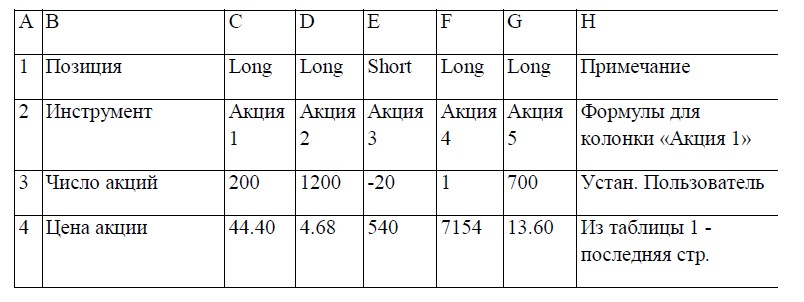
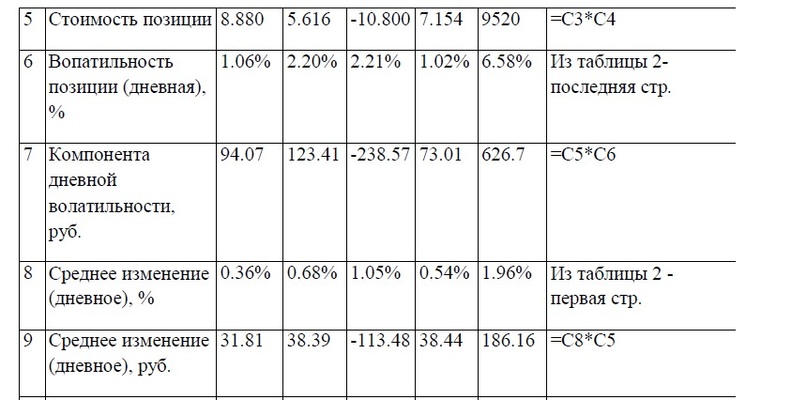
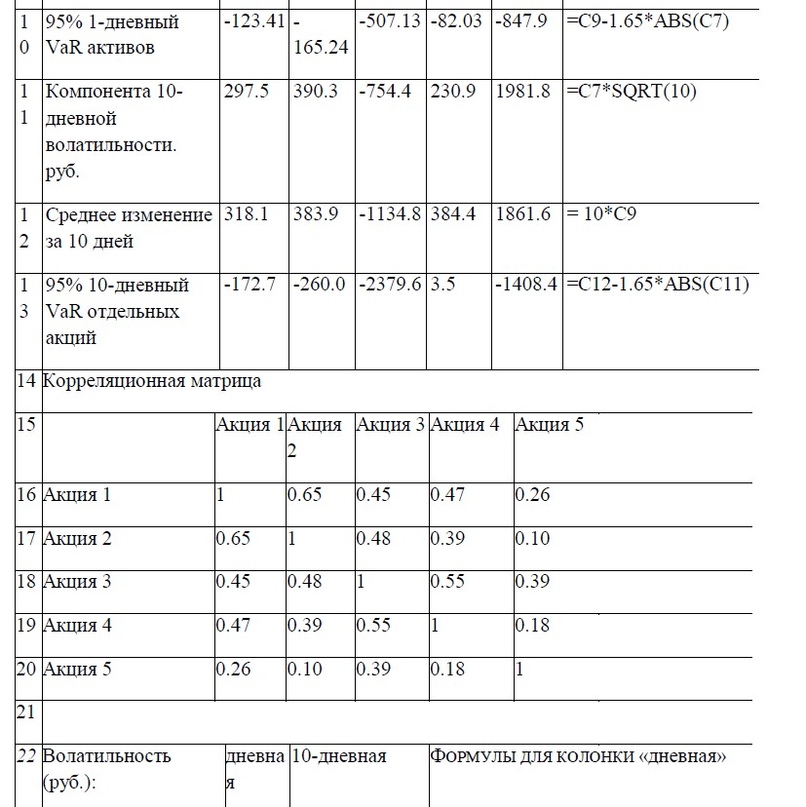
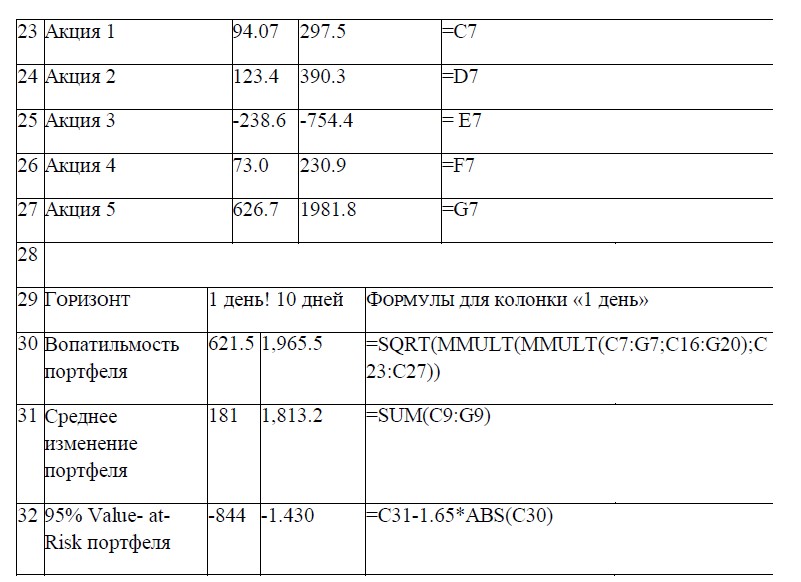
Протокол расчета, позволяющий видеть все промежуточные этапы, представлен в таблице 3. Здесь же даны формулы, с помощью которых производятся вычисления.
Следует иметь в виду: данная таблица есть копия рабочего листа Excel, поэтому при написании программы рекомендуется придерживаться указанного порядка, пользуясь для подсказки формулами, выложенными в крайней колонке «Н» справа. Позже, если возникнет желание, структуру таблицы можно изменить.
Остается сделать ряд важных замечаний
Во-первых, в зависимости от задачи число входящих в портфель активов можно увеличить или уменьшить.
Во-вторых, при оценке по ценам внутри дня при вычислениях надо придерживаться единого масштаба, поэтому VaR будет получаться для задаваемого числа часов в параметре «время». Для перевода в дневной масштаб следует учесть число торговых часов в одном дне.
Для обращающихся на бирже активов обычно это не вызывает трудностей, но в ряде случаев можно столкнуться с проблемами. Как, скажем, на рынке FOREX, где трудно предложить однозначное решение, поскольку приходится учитывать неравномерный характер торговой активности.
В-третьих, следует иметь в виду: портфель может содержать различные активы. Единственное условие – они должны быть выражены в одной валюте.
Например, если бы мы пожелали оценить риск портфеля, состоящего из акций в рублях, валютной позиции по евро/доллар и процентного фьючерса в британских фунтах, нам пришлось бы прежде выбрать счетную валюту.
Если мы выбрали евро, то потребуется пересчитать все ценовые ряды в евро по соответствующему курсу для каждого дня. После этого нам удастся без труда получить результирующую цифру, которая также будет в евро.
Шаг 4. Оптимизация портфеля
Поняв процедуру оценки риска, можно решать такие серьезные задачи, как поиск более эффективных решений. В Excel существует опция «Solver» в разделе «Tools», позволяющая выполнять поиск решений по заданным условиям. О других полезных функциях Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Например, если мы укажем, что нас устраивает иное значение 95% VaR – скажем, -500, а не -844 – и определим при этом возможность изменения числа всех акций, то программа вычислит: «Акция 1» следует иметь 119 акций, «Акция 2» – 1193, «Акция 3» – 11, «Акция 4» – 2 и «Акция 5» – 227 акций. Причем с длинными позициями по всем бумагам.
Легко заметить: подобный подход отличается ограниченностью, поскольку мы никак не определяем имеющийся в нашем распоряжении капитал, а указываем лишь уровень принимаемого риска.
Эта проблема легко разрешима: имеющиеся данные позволяют производить любые вычисления, необходимые для определения стоимости портфеля, а также размера требуемого капитала как при торговле с маржой, так и без нее. После этого определить степень риска в относительных величинах не представляет труда, это будет частное от VaR и рабочего капитала или размера счета – в зависимости от того, что необходимо оценить.
С полученной величиной мы можем обращаться точно так же, как и со значением VaR в денежных единицах. Скажем, если нам для создания портфеля, представленного в таблице 3, потребуется капитал в размере 42 тыс. руб. (исходя из правил брокера), то 1-дневный 95% VaR составит 2.01%, а 10-дневный – 3.41%.
Данные цифры говорят: существует 95%-ная вероятность, что потери портфеля за 1 день не превысят 2.01% от работающего капитала, а за 10 дней – 3.41%. Естественно, если нам нужна более полная картина, следует проводить расчеты также и для всего капитала, с учетом резервов.
Опираясь на эти цифры, можно выполнять оптимизацию, пользуясь алгоритмом, описанным выше. Например, задавая 1-дневные потери в размере 1% от работающего капитала при доверительном уровне в 95%, мы узнаем, что это достигается за счет увеличения короткой позиции в «Акция 3» (с 20 до 23 акций) и покупки 18, а не одной, акций «Акция 4», при неизменности числа прочих бумаг.
Обратите внимание: не введя в данную процедуру ограничений на капитал, мы обнаружим, что эта возможность для нас нереальна или не отвечает нашим намерениям, поскольку для создания портфеля требуется 163 тыс. руб. Поэтому следующий этап усложнения алгоритмов оценки риска – ввод ограничений.
Шаг 5. Ввод ограничений
Ввод ограничений, позволяющих решать проблему оптимизации, требует немного больше знаний об электронных таблицах. Полностью описать то, как можно решить ту или иную задачу, здесь не представляется возможным.
Во-первых, можно найти немало подходящих алгоритмов, позволяющих достичь поставленной цели. Во-вторых, многие из них связаны с уровнем квалификации инвесторов – пользователей среды Windows, а обучение не является нашей задачей. В-третьих, как показывает практика, пользователям лучше всего самостоятельно создавать интерфейс, если работа ведется с Excel.
Поэтому в шаге 5 только указывается путь, ведущий к построению потокового процесса контроля над риском и управления им.
Наиболее простой способ решить задачу – ввести условия, опираясь на соотношение между показателем меры риска и размером имеющегося в нашем распоряжении капитала. Если одновременно мы хотим автоматизировать процесс, нам потребуется ввести дополнительные ограничения, описывающие наши реальные возможности. Обычно это реализуется через совместное использование таких функций, как «=IF(), OR(), AND()».
Дополнительные возможности появляются, если изменениям будет подвергаться не число акций, а их доля в портфеле. Описание связей в таком случае будет легче, так как мы заранее указываем размер капитала, под который формируется портфель. Число акций уже будет не задаваться пользователем, как это предложено в таблице 3, а вычисляться на основе весовой доли в портфеле.
Причем подходы, основанные на оценке веса, могут иметь и другие решения. Вводя граничные условия с целью автоматизации процесса оценки риска, мы неминуемо столкнемся с проблемой управления резервами.
И здесь следует обратить внимание на важную деталь. Дело в том, что непосредственное применение VaR – это определение, какой капитал необходимо резервировать, чтобы иметь достаточное покрытие рыночного риска. В практике рядового инвестора – это решение вопроса, сколько надо иметь свободных средств на счете, чтобы не потерять свыше заданной величины или не получить margin call (при маржевой торговле).
В банковской практике рекомендуемые резервы – 3-кратный 10-дневный 99% VaR (для портфеля из таблицы 3 такие резервы составят 8299 рублей). Поскольку резервы, оцениваемые через VaR, – величина «плавающая» и зависит от волатильности, этот аспект может оказаться для кого-то привлекательным. В таком случае вполне естественно включить данный параметр в алгоритмы, обеспечивающие обсчет риска.
Наконец, следует включить и ожидаемую прибыль. Это дополнение позволяет получать новые оценочные коэффициенты, играющие важную роль в торговой практике. Скажем, мы можем вывести соотношение «прибыль/возможный убыток». Если при этом учтены издержки на транзакции, а также соответствуют горизонты, использованные для оценки потерь и прибыли, то у нас получится формулировка для оценки рисков RAROC по методике Bankers Trust.
Решений автоматизации процедур, связанных с риск-менеджментом, существует много. Окажутся ли они эффективными, в значительной степени зависит от точности поставленной задачи и желания получить действительно простую и понятную процедуру оценки меры риска.
Вершиной здесь является построение потокового процесса управления ценовыми и финансовыми рисками, решающего с максимально возможной эффективностью основную задачу инвестора – как понадежней заработать.
Автор: Михаил Чекулаев