Пролог
Вы можете себе представить телевизионную новостную передачу или выпуск политического шоу без фразы «Согласно статистике…»?
Или же совещание на работе, во время которого глава какого-нибудь отдела не утверждает так: «Цифры говорят нам, что…»?
Или в журналах и газетах Вы не встречали «раскрывающие шокирующую правду» заголовки типа: «По данным интернет-опроса 100% людей пользуются интернетом»?
Сейчас сплошь и рядом мы слышим: «Цифры не врут», «Статистика — полезный инструмент в ведении бизнеса» и так далее.
Статистика — очень хитрая наука. Как говорил французский писатель Гюстав Флобер: «…самая точна из всех неточных». Поэтому в неумелых руках она страшна, а вот в руках специалиста…опасна вдвойне.
Мы решили подобрать несколько интересных примеров того, как с помощью статистики можно обмануть и заставить верить в абсурдные вещи.
В среднем, голубцы
В статистике существует много методов работы с данными и представления их пользователю. Один из хитрейших способов запутать человека – рассказать ему о «среднем». Каждый интуитивно понимает, что среднее значение – сумма всех чисел, деленная на количество этих чисел. Но это не всегда очевидно.
Есть даже анекдотический рассказ на эту тему:
«Преподаватель рассказывает студенту о понятии «среднее», его пользе для расчетов и описания экспериментов. Но, видя, что аудитория его не понимает, пробует привести простой пример из жизни. − Давай, − говорит он студенту, − пойдем на улицу, встанем перед ВУЗом и посчитаем сто первых людей, которые пройдут мимо. Ты увидишь, что, в среднем, примерно 50 из них будет мужчинами, и 50 – женщинами. Они вышли на улицу, посмотрели налево, вперёд, направо – улица была пуста. Они обернулись, а из-за поворота им навстречу, чеканя шаг, маршировала рота солдат…». И такие случаи в статистике не редкость.
Рассмотрим следующую ситуацию: крупной фирме необходимо рассчитать, какова средняя зарплата сотрудника. Пусть генеральный директор получает 25 тысяч условных единиц в месяц. Его заместитель довольствуется 7,6 тысячами. Топ-менеджеры зарабатывают 5,5 тысяч, менеджеры среднего звена по 3,5 тысячи, младшие менеджеры – 2,5 тысячи, а обычные работники по 1,4 тысячи в месяц. Напомним, что задача заключается в представлении компании в лучшем свете, а не в передаче достоверных фактов.
Так вот, «среднее значение» можно посчитать далеко не одним способом.
Чтобы найти среднее арифметическое всех зарплат, нужно найти среднее, как его все и понимают. Все просто. Мы получим, что средняя зарплата равна 3,472 тысячи условных единиц. Заметим, что это очень большое значение плохо отражает действительность относительно обычных работников. Это вышло из-за того, что у начальников огромные зарплаты, у сотрудников маленькие, а в целом получается неплохо.
Этой ситуации в народе соответствует всеми любимая фраза «Средняя температура по больнице» или «Чиновники едят мясо, я — капусту. В среднем мы едим голубцы».
Другой результат получится, если в качестве «среднего» мы будем считать медиану. Медиана – число, которое делит набор чисел «пополам». Например, в «1,2,3,4,5» медиана – 3; а в «1,2,3,4» – 2.5.
Проще говоря, одна половина сотрудников получает зарплату больше какого-то значения, а другая половина – меньше.
Таким образом, получаем, 2.1 тысячи. Это уже больше похоже на правду, так как несет больше информации об обычных работниках. Точнее, это число показывает, как зарплата рядовых сотрудников соотносится с остальными.
Самый правдоподобный, но не выгодный для компании вариант – в качестве «среднего» брать моду – число, чаще всего встречающееся в наборе чисел. Так как простых работников больше, чем всех остальных, то мода будет соответствовать их зарплате: 1.4 тысячи условных единиц.
Мы рассмотрели случай, когда брали реальные данные, по-разному их «вертели» и получали правильные, с точки зрения математики, результаты. А часто бывает, что первоначальная информация уже искажает действительность.
О бедных и богатых
Будучи студентом или выпускником Вы никогда не обращали внимание на информацию в прессе о чересчур завышенных зарплатах ровесников?
В своей книге «How to Lie with Statistics» Дарелл Хафф говорит, что это очень старая проблема: такой же вопрос возникал у выпускников Yale (Йельский университет) 1924-го года. Они утверждали, что доход их современников сильно завышен.
Все претензии были предъявлены к СМИ. Но выяснилось, что собранные при опросе данные были верными: все участники говорили правду. Вот только выборка данных с самого начала была некорректной.
Дело в том, что опрос в то время происходил по почте (кандидатам присылали письма с вопросами), но далеко не все отправляли ответы, а лишь небольшая часть.
К тому же, охотнее участвовали те, у кого дела шли хорошо (что равнялось «удалось устроиться на высокооплачиваемую работу»). Поэтому читателям предоставили слишком хорошую статистику, что и вызвало такое возмущение.
То есть такой подход привел к искажению выборки и превратил результаты опроса в абсолютно бесполезные.
Такие ошибки в статистике встречаются чаще остальных, ведь главное условие – независимая, случайная выборка. Незнающие «специалисты» могут даже не обратить внимание на факторы, которые могут привести к неправильному сбору данных.
Предвзятые выборки – основные источники искаженных результатов исследований.
Так, например, случилось в США в 1948 году на выборах президента. Газета Chicago Tribune сразу после закрытия выборных участков провела опрос, чтобы объявить предварительный исход выборов.
Информация, собранная путем обзвона избирателей, предвещала победу Дьюи с большим преимуществом относительно Трумана.
Именно тогда Chicago Tribune опубликовала свой знаменитый заголовок «DEWEY DEFEATS TRUMAN» (Дьюи побеждает Трумана). Но, как всем известно, после выборов 1948 года президентом США все же стал Труман. Что же пошло не так?!
Дело в том, что людей обзванивали случайным образом, и количество опрошенных тоже было достаточно, но организаторы не учли тот факт, что в те годы телефон могли себе позволить только граждане с высоким уровнем жизни (редко средство связи встречалось у людей с низким достатком).
Труман представлял интересы демократов, а среди них, как правило, много тех, кому телефон не доступен. Отсюда и пошло искажение выборки, которое привело к ложному прогнозу.
Мы уже поняли, как важны непредвзятые выборки для правильности исследований; увидели, какие тайны скрыты за понятием «среднее». А сейчас мы убедимся, что даже независимая выборка и правильно подобранное «среднее», может запутать еще больше и даже привести к ошибкам!
Одинаковое разное
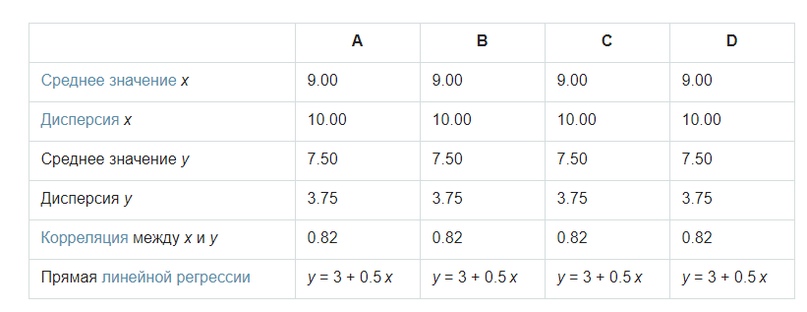
В 1973 году английский математик Ф. Дж. Энскомб нашел необычное явление, которое стало называться Квартетом Энскомба. В чем же его суть? Ученый взял четыре набора, состоящих из 11 пар чисел. Выяснилось, что у всех наборов основные статистические свойства, такие как среднее значение, дисперсия, прямая линейной регрессии и корреляция, идентичны.
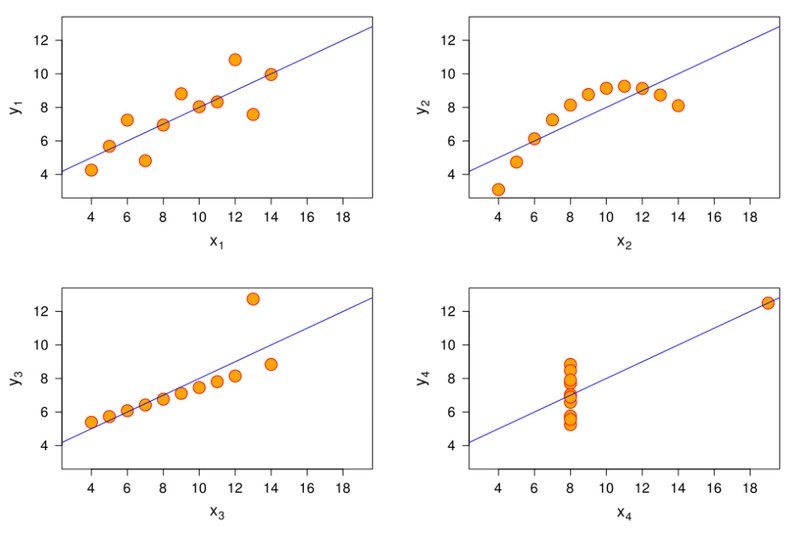
То есть с точки зрения математики – это четыре одинаковые выборки. Но не все так просто. Вот как выглядят эти четыре набора точек:
Мы видим, что графики наборов данных, имеющих одинаковые параметры, существенно различаются. Без наглядной демонстрации трудно было бы отличить наборы друг от друга и понять их особенности.
Естественно, это не пробел в статистике – различие между четырьмя выборками есть: такие результаты получаются при «грубом» исследовании.
Такой парадокс заставляет нас немного поломать голову над вопросом: как такое может быть? А тем временем, маркетологи уже давно поняли важность визуализации для достижения своих коварных целей.
Немного новостей и фруктов
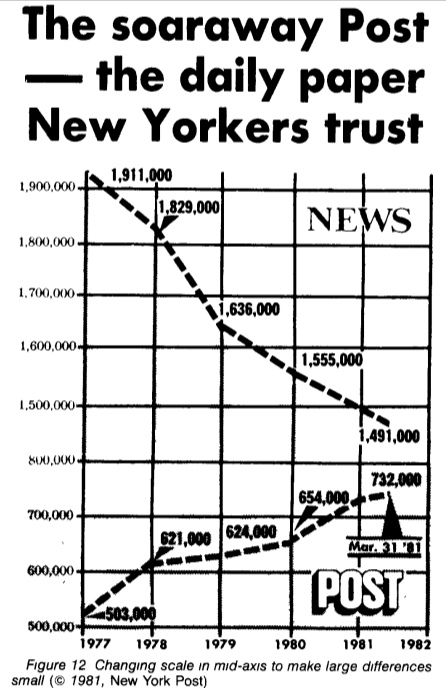
Если по годовому плану фирма должна была догнать своих конкурентов, но у них «чуть-чуть» не получилось, то как преподнести этот факт начальству, чтобы он не заметил неблагоприятную новость? На это вопрос ответил New York Times, опубликовавший такой график:
На первый взгляд, может показаться, что Post молодцы, догнали News! А вот если посмотреть на вертикальную шкалу, то сразу в глаза бросается скачок с 800 тысяч до 1,500 тысяч. То есть если сделать правильный масштаб графика, то разрыв между компаниями будет выглядеть значительно больше.
Такая манипуляция с графикой – довольно популярный прием среди экономистов и финансистов.
Представляем еще несколько примеров лжи или приукрашивания с помощью графиков и гистограмм:
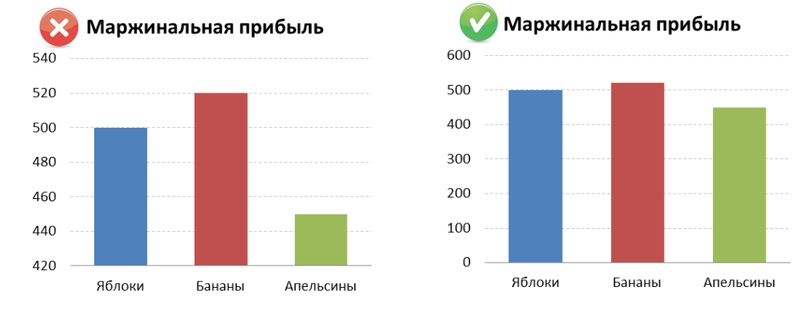
- Начинать вертикальную ось не с 0
Если посмотреть на левую картинку, то может сложиться ощущение, что бананы приносят прибыли в 3 раза больше, чем апельсины, а вот яблоки – в 2 раза. Опытный пользователь сразу обратит внимание на вертикальную шкалу и заметит, что она начинается не с 0, а это искажает восприятие.
Конечно, это не ошибка, диаграмма нарисована правильно. Excel порой сам выбирает более красивый вариант визуализации. Но согласитесь, посмотрев на правый и левый график можно сделать разные выводя, хотя отображают они одни и те же данные.
2. Временная ось искажает целостность периода
На левом графике видно, что продажи идут хорошо, продажи наблюдаются в каждом месяце (они даже увеличиваются). Неопытный или невнимательный сотрудник сделает именно такой вывод.
А вот на правой диаграмме ситуация уже не такая красивая: оказывается, за два месяца вообще не было продаж. Такая уловка, порой тоже может сработать, если нас хотят сбить с толку.
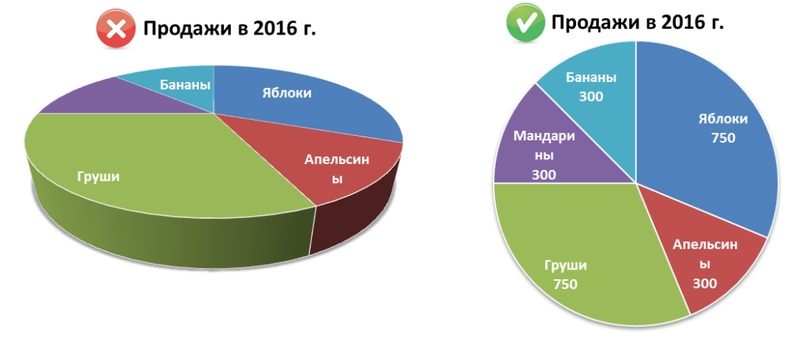
3. Использование 3D эффектов
Этот прием очень коварный. Происходит дезориентация пользователя. Становиться трудно определить пропорциональное отношение частей.
С помощью этих и других возможностей Excel можно легко манипулировать выводами людей, полагаясь на их невнимательность, что вполне оправданно, ведь мы очень редко всматриваемся, внимательно изучаем текст, таблицы, графики. Рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel», если хотите узнать больше о работе в программе.
Увидев половину, мы уже готовы сделать заключение, додумав остальное самостоятельно. Этим и пользуются хитрые специалисты.
Эпилог
«Существуют три вида лжи: ложь, наглая ложь и статистика». К сожалению, так до конца и не понятно кому принадлежит эта замечательная «острая» фраза, отражающая всю суть статистики.
Этот инструмент остается загадкой, обманом, фокусом для многих людей. Но несмотря на это, без него многие процессы были бы невозможны. Поэтому, какими бы необъяснимыми порой не казались статистические выводы, мы продолжаем активно использовать эту науку.
Данная подборка показывает далеко не все приемы, в которых специально или неосознанно искажают факты. Но прежде всего, она призывает внимательнее относиться к статистическим данным и выводам.
P.S.
А Вы знали, что дни рождения полезны для здоровья?! Нет? А ведь это именно так! Британские учёные доказали, что те, у кого было больше дней рождения, как правило, жили дольше… Интересный факт, не правда ли?
