Туториал: нейросети для алгоритмической торговли
 6 мин
6 мин
 8750
8750  8 Июн 2020
8 Июн 2020 
Основатель и Генеральный директор, SF Education

Получите 3-х дневный бесплатный демо-период
Этот материал посвящен прогнозированию временных рядов с помощью нейросетей. Для анализа были выбраны самые непредсказуемые данные – финансовые. Способна ли нейронная сеть уловить паттерны в абсолютно случайном наборе информации и предвидеть события рынка?
Демонстрация производится на модели многослойного перцептрона. Про альтернативные архитектуры, например, сверточные или LSTM, можно узнать из другого материала автора. В статье также рассматривается феномен переобучения нейросети, который часто наблюдается при работе со случайными величинами.
Описанный алгоритм действий от обработки временных рядов до валидации результатов обучения можно применять к другим типам данных и задачам классификации. Чтобы увидеть рабочий пример, скачайте IPython Notebook. Если вы еще не начали изучать Python, то советуем начать с нашего открытого онлайн-курса «Первый код на Python».
Подготовка финансовых данных
Для исследования отлично подойдут исторические данные о стоимости акций компании Apple в период с 2005 по 2017 год. Скачать файл в формате csv можно из Yahoo Finance. Прежде всего, нужно подключить к проекту некоторые библиотеки:
import matplotlib.pylab as plt import numpy as np import pandas as pd
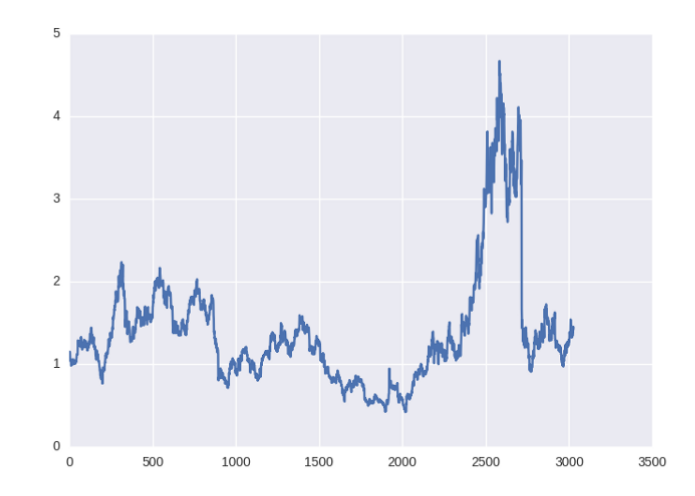
Цены 2017 года находятся в самом начале файла. Для обучения нужно выстроить данные в хронологическом порядке (с помощью команды [:-1]). Сразу же создадим график изменений:
data = pd.read_csv('./data/AAPL.csv')[::-1] close_price = data.ix[:, 'Adj Close'].tolist() plt.plot(close_price) plt.show()
Прогнозировать временные ряды финансовых данных можно двумя способами. Речь идет о базовом прогнозе без учета аномалий, волатильности и прочих интересных параметров.
- Бинарная классификация. Простое определение направления движения цены: вверх ([1; 0]) или вниз ([0; 1]).
- Регрессия. Попытка предугадать цену на завтрашний день, то есть числовое значение. При этом потребуется нормализация значений.
В качестве входной информации используется окно временного ряда размером в 30 дней. На его основе нейросеть постарается предсказать изменение цены на 31-й день.
90% имеющихся исторических данных будет использовано для обучения нейросети. Оставшиеся 10% послужат тестом для проверки модели.
Главная сложность работы с финансовыми данными заключается в их нестационарности. Статистические характеристики подобных временных рядов, такие как математическое ожидание, средние значения и дисперсия, изменяются с течением времени. Это подтверждает тест Дики — Фуллера. Подобная особенность не позволяет применять для нормализации классические методы, например, minmax или Z-score.
Однако для классификации точные цифры не требуются, поэтому дисперсия и математическое ожидание не имеют особого значения. Здесь можно рискнуть и использовать z-score, не затрагивая информацию из будущего.
X = [(np.array(x) - np.mean(x)) / np.std(x) for x in X]
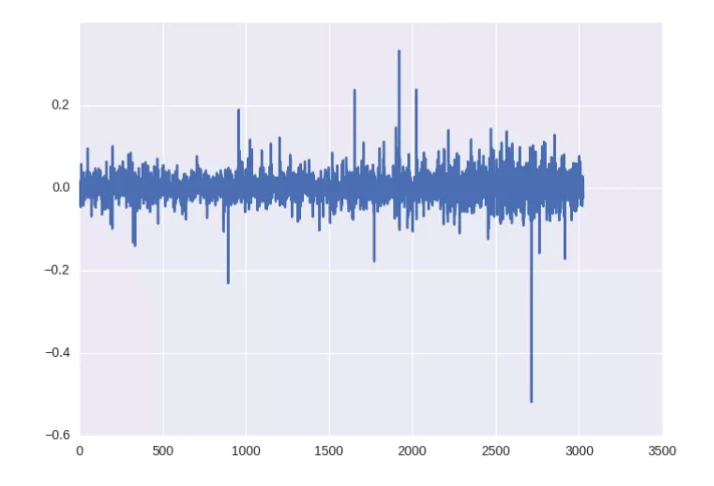
С регрессией так не получится, но для нормализации можно использовать изменение цены в процентах.
close_price_diffs = close.price.pct_change()
Вот так без особых фокусов со статистическими параметрами удалось получить нормализованные данные в пределах от -0.5 до 0.5.
Архитектура нейронных сетей
В качестве базовой модели для обучения будет использоваться многослойный перцептрон. Ознакомиться с базовыми понятиями работы нейросетей можно здесь.
MLP позволит продемонстрировать, как просто переобучить сеть на случайных финансовых значениях, а также как с этим бороться.
При необходимости эти идеи легко расширить на сверточные или рекуррентные модели, важно лишь понять основную концепцию. Для прототипирования используется Keras — простой и удобный фреймворк, который позволяет гибко настраивать процесс обучения.
Первый вариант простой нейросети:
model = Sequential() model.add(Dense(64, input_dim=30)) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(2)) model.add(Activation('softmax'))
Во входном слое 30 нейронов, что соответствует длине окна. Еще 64 — в первом скрытом слое.
Для регрессии будет установлен другой параметр активации — linear.
Рекомендуется после каждого аффинного или сверточного слоя использовать batch нормализацию, а в качестве основной функции активации выбирать Leaky ReLU (выпрямитель с утечкой). Это позволяет значительно ускорить обучение и уже стало стандартом.
Для классификации параметру loss устанавливается значение кросс-энтропии (categorical_crossentropy), а для регрессии — среднеквадратической ошибки (mse).
Хорошей практикой является снижение скорости обучения, если нет улучшения. Это осуществляет функция ReduceLROnPlateau:
reduce_lr = ReduceLROnPlateau(monitor='val_loss',
factor=0.9,
patience=5,
min_lr=0.000001,
verbose=1)
model.compile(optimizer=opt,
loss='categorical_crossentropy',
metrics=['accuracy'])Обучение начинается:
history = model.fit(X_train, Y_train,
nb_epoch = 50,
batch_size = 128,
verbose=1,
validation_data=(X_test, Y_test),
shuffle=True,
callbacks=[reduce_lr])А это код для визуализации результатов, который будет создавать графики изменения точности и ошибки.
plt.figure()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='best')
plt.show()
plt.figure()
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel(‘acc’)
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='best')
plt.show()Обратите внимание, что для получения адекватного результата обучение должно длиться хотя бы 50−100 эпох. В ином случае сеть просто изучит распределение, используемое для тренировки, но не сможет находить паттерны в тестовой выборке.
Классификация
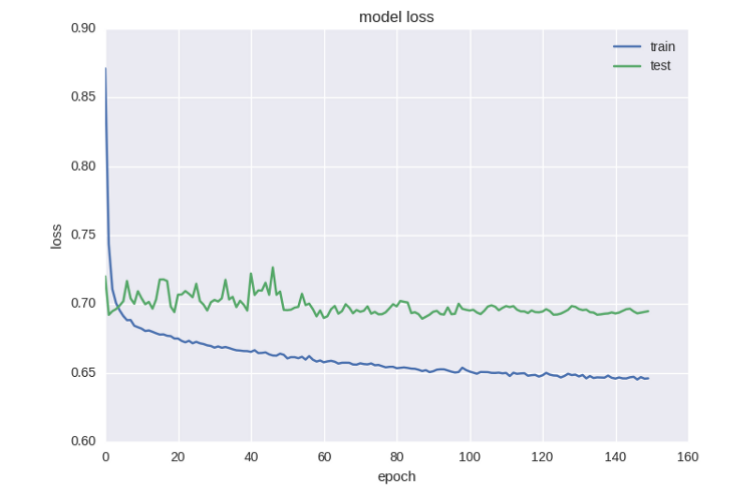
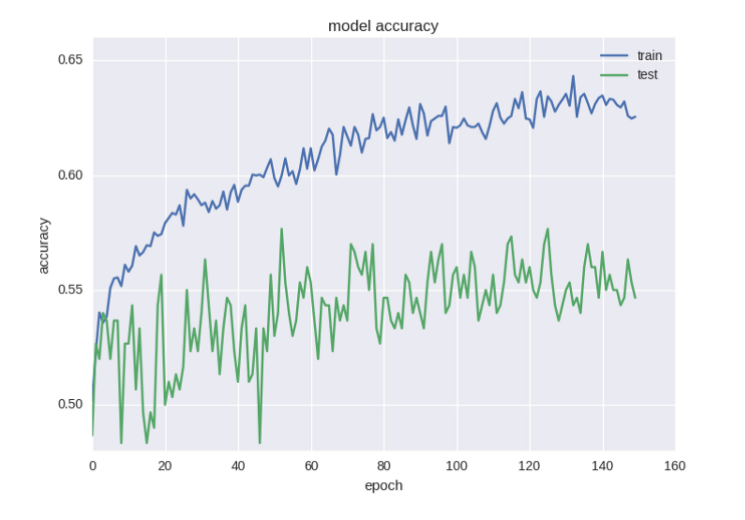
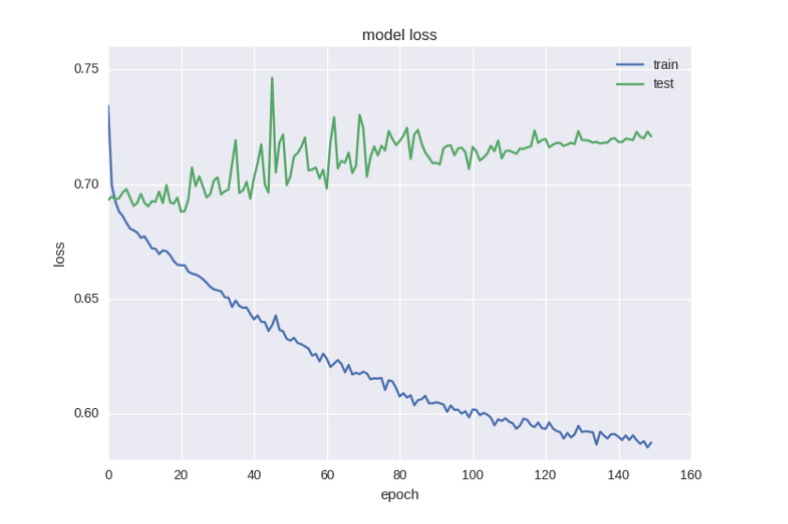
Первая проверка модели:
Выглядит не очень хорошо. Налицо явное переобучение нейросети. В тренировочной выборке точность резко возрастает, а величина ошибки падает.
Возможно, следует добавить еще слой в модель, сделав ее более глубокой:
model = Sequential() model.add(Dense(64, input_dim=30)) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(16)) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(2)) model.add(Activation('softmax'))
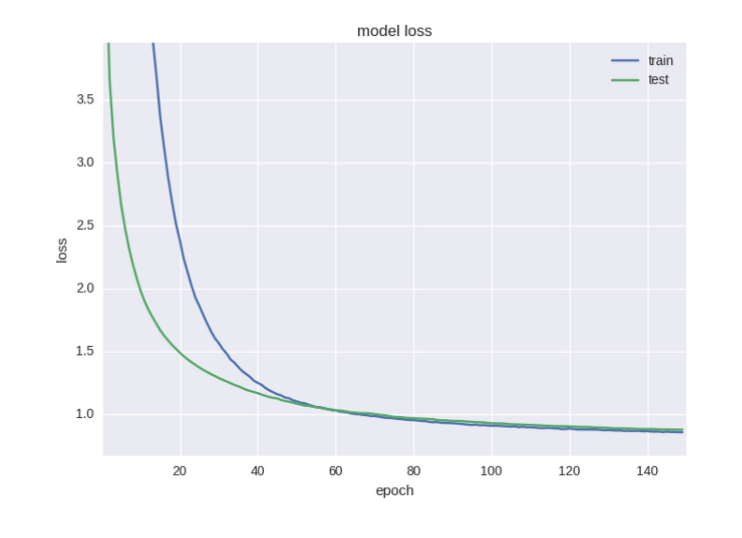
Новые результаты также не впечатляют:
Ничего не изменилось, даже стало хуже, чем раньше.
Пришло время регуляризировать сеть, чтобы справиться с переобучением. На веса нейросети при этом накладываются некоторые ограничения и часть из них обращается в ноль.
Чаще всего это достигается путем добавления к функции ошибки L2 нормы по сумме весов. В Keras для этого используется функция keras.regularizers.activity_regularizer.
model = Sequential() model.add(Dense(64, input_dim=30, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(16, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(2)) model.add(Activation('softmax'))
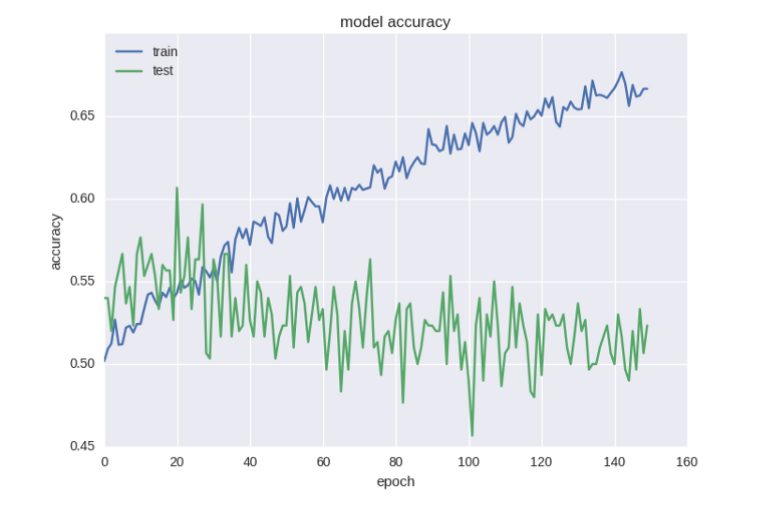
Уже лучше, но все-таки недостаточно хорошо. Ошибка уменьшилась, но с точностью проблемы. Такой эффект при работе со случайными данными — не редкость, и здесь это очень хорошо объясняется.
В общих чертах можно сказать, что это вызвано высоким уровнем шума. Ошибка рассчитывается на основе cross-entropy, а точность — это индекс нейрона с правильным ответом. Ошибка может уменьшаться, а индекс при этом все равно остается неправильным.
В уже упорядоченную сеть можно ввести еще больше регуляризации с помощью техники «прореживания» (Dropout). При обучении некоторые веса будут случайным образом игнорироваться. Метод используется для борьбы с коадаптацией нейронов и эффектом переобучения.
model = Sequential() model.add(Dense(64, input_dim=30, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dropout(0.5)) model.add(Dense(16, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(2)) model.add(Activation('softmax'))
Не рекомендуется проводить прореживание сразу после входного слоя, а также прямо перед выходом. В данной модели оно будет происходить между двумя скрытыми слоями.
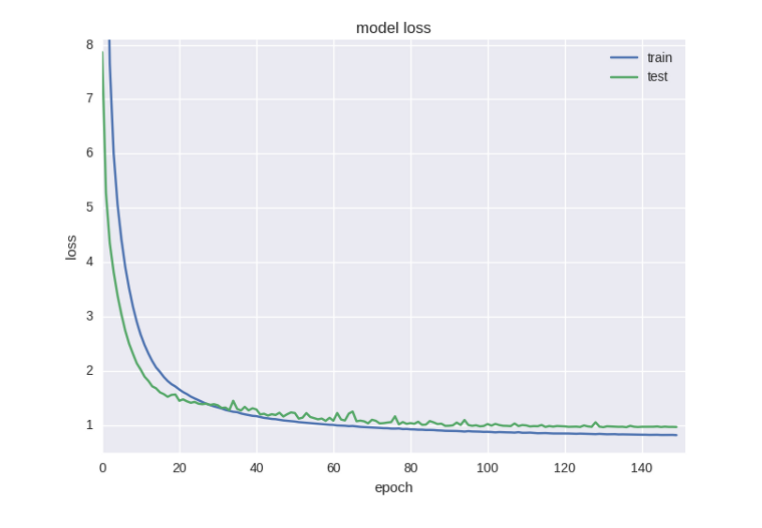
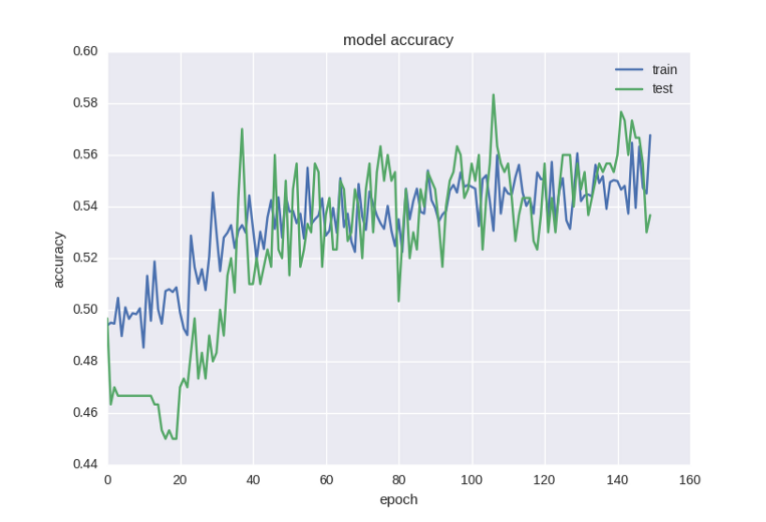
Вот теперь графики стали вполне правдоподобными. Если немного раньше приостановить обучение, можно получить 58% точности прогноза. Это уже намного полезнее случайного угадывания.
Ради интереса вы можете попробовать предсказать движение цены акций через некоторый промежуток времени, например, через 5 дней. Как справляется нейросеть с этой задачей: лучше или хуже, чем с однодневным прогнозом? Почему так происходит?
Регрессия
Полученная архитектура модели уже доказала, что способна выучить необходимые признаки. Для решения регрессионной задачи из нее следует убрать dropout и увеличить количество итераций:
Получается вот такая архитектура:
model = Sequential() model.add(Dense(64, input_dim=30, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(16, activity_regularizer=regularizers.l2(0.01))) model.add(BatchNormalization()) model.add(LeakyReLU()) model.add(Dense(1)) model.add(Activation('linear'))
Также нужно построить график для визуального определения точности прогнозов:
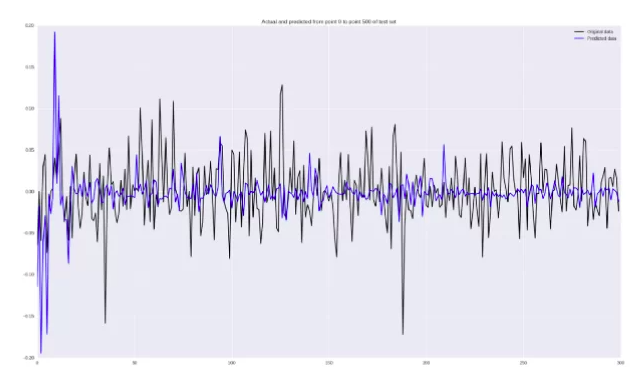
pred = model.predict(np.array(X_test)) original = Y_test predicted = pred plt.plot(original, color='black', label = 'Original data') plt.plot(predicted, color='blue', label = 'Predicted data') plt.legend(loc='best') plt.title('Actual and predicted') plt.show()
Да, работает он неважно. Кое-где действительно угадывается тренд, но в целом точность плохая. В заключительной части статьи приведено несколько методов, способных улучшить качество регрессионного прогнозирования.Проверка на истории
Все эти разработки проводятся для того, чтобы в конце концов создать эффективную торговую систему, способную заключать сделки и получать прибыль.
Для бэктестинга стратегий (проверка на исторических данных) существует ряд готовых инструментов, например, Quantopian. Если вам интересно, как они реализованы изнутри, обратите внимание на эту книгу.
Стратегия применения созданной нейросети очень проста: при поступлении прогноза роста цен, трейдер покупает акции, а если сеть предсказывает скорое падение, то продает.
if np.argmax(pred) == 0 and not self.long_market:
self.long_market = True
signal = SignalEvent(1, sym, dt, 'LONG', 1.0)
self.events.put(signal)
print pred, 'LONG'
if np.argmax(pred) == 1 and self.long_market:
self.long_market = False
signal = SignalEvent(1, sym, dt, 'EXIT', 1.0)
self.events.put(signal)
print pred, 'EXIT'
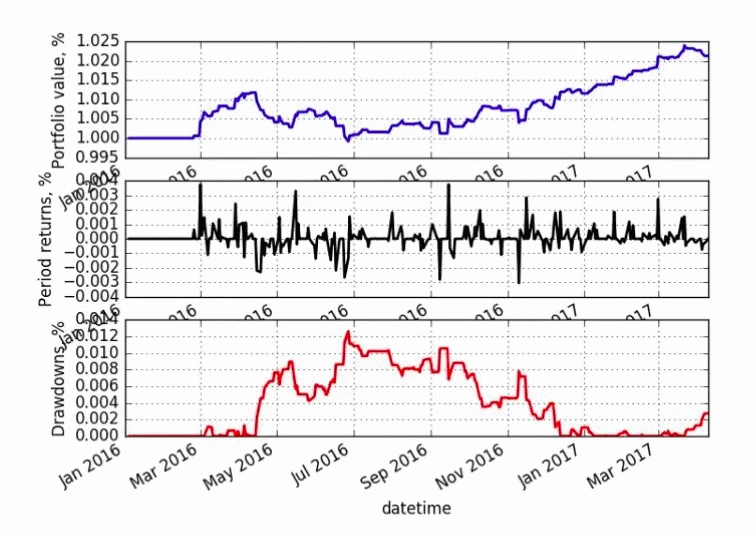
Нейросеть обучалась на данных 2012–2016 годов и тестировалась на 2016–2017 годах.
Первый график демонстрирует рост стоимости портфеля (потрясающе! целых 3% за полтора года!), черная линия говорит об активности, а красная обозначает периоды потери денег.
Обсуждение
Кажется, что результаты обучения очень плохи. Регрессия совершенно ужасная, да и 58% точности в классификации не впечатляют. Что уж говорить о «невероятном» доходе в 3%. Честное слово, проще было купить акции компании Apple и просто удерживать их. За это время они выросли на 20%.
После таких результатов хочется закрыть ноутбук и заняться чем-нибудь, не связанным с финансами и машинным обучением.
Но не спешите. Существует много способов улучшить результаты до 60−70%:
- Использование более высокочастотных данных. Вместо ежедневных значений следует брать ежечасные или даже ежеминутные. Алгоритмы машинного обучения более эффективны на коротких временных отрезках, к тому же таким образом они получат больше паттернов.
- Оптимизация параметров обучения. В демонстрационном примере все характеристики модели были выбраны совершенно случайно. Возможно, следует взять 45-дневные окна и увеличить количество нейронов в скрытых слоях нейросети. Определить это поможет случайный поиск.
- Применение других архитектур. Более продвинутые сверточные или рекуррентные нейросети могут дать лучший результат.
- Анализ всех имеющихся данных. Недостаточно лишь цены закрытия для построения эффективной финансовой модели. В том же csv-файле содержится еще много другой полезной информации, которую тоже можно анализировать. Чем больше данных, тем точнее прогнозы.
- Использование других функций потерь, возможно, асимметрических. Используемая в примере MSE не обращает внимания на знак полученного числа, несмотря на то, что он очень важен для решения.
Выводы
Прогнозировать финансовые данные непросто, но возможно. Это исследование с некоторыми правками может стать хорошей отправной точкой для создания эффективного торгового инструмента.