Что такое регрессионный анализ?
 5 мин
5 мин
 13582
13582  16 Дек 2020
16 Дек 2020 
Основатель и Генеральный директор, SF Education

Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. По сути, регрессионные методы показывают, как по изменениям «независимых переменных» можно зафиксировать изменение «зависимой переменной».
Зависимую переменную в бизнесе называют предиктором (характеристика, за изменением которой наблюдают). Это может быть уровень продаж, риски, ценообразование, производительность и так далее. Независимые переменные — те, которые могут объяснять поведение выше приведенных факторов (время года, покупательная способность населения, место продаж и многое другое).
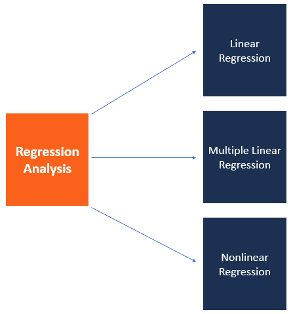
Регрессионный анализ включает несколько моделей. Наиболее распространенные из них: линейная, мультилинейная (или множественная линейная) и нелинейная.
Как видно из названий, модели отличаются типом зависимости переменных: линейная описывается линейной функцией; мультилинейная также представляет линейную функцию, но в нее входит больше параметров (независимых переменных); нелинейная модель — та, в которой экспериментальные данные характеризуются функцией, являющейся нелинейной (показательной, логарифмической, тригонометрической и так далее).
Чаще всего используются простые линейные и мультилинейные модели.
Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы. Кстати, регрессионный анализ можно проводить с помощью языка R. Сделать первые шаги в освоении этого языка поможет наш открытый курс «Аналитика с SQL и R».
Рассмотрим поподробнее принципы построения и адаптации результатов метода.
Предположения линейной модели
Линейный регрессионный анализ основан на шести фундаментальных предположениях:
- Переменные показывают линейную зависимость;
- Независимая переменная не случайна;
- Значение невязки (ошибки) равно нулю;
- Значение невязки постоянно для всех наблюдений;
- Значение невязки не коррелирует по всем наблюдениям;
- Остаточные значения подчиняются нормальному распределению.
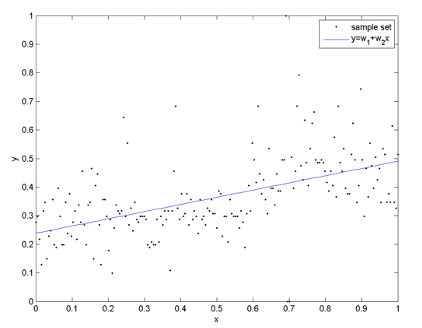
Построение простой линейной регрессии
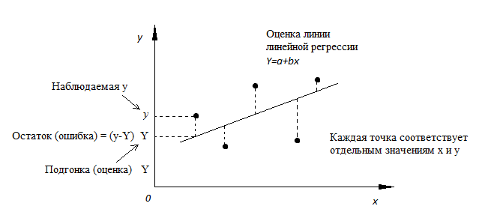
Простая линейная модель выражается с помощью следующего уравнения:
Y = a + bX
Где:
- Y – зависимая переменная
- X – независимая переменная (объясняющая)
- а – свободный член (сдвиг по оси OY)
- b – угловой коэффициент. Он указывает на поведение кривой (убывает или возрастает, угол между с осью)
a и b называют коэффициентами линейной регрессии. В их нахождении и заключается основная задача.
Если в нашей задаче присутствуют несколько факторов: x1,
x2,
x3, от которых, мы полагаем, зависит y, то нужно использовать множественную регрессию, описываемую уравнением:
Y = a + b1 x1 + b2 x2 + b3 x3
Существует много способов определить коэффициенты a и b. Но самым простым и надежным является метод наименьших квадратов (можно научно доказать, что это лучший способ).
Идея метода: мы имеем значения y – числовой ряд или набор данных. Необходимо построить функцию регрессии Y=a + bX так, чтобы выражение (Y – y)2 было минимальным. (Y – y)2 – ошибка, которую мы хотим минимизировать. Минимизируется функционал благодаря подбору коэффициентов a и b.
Ключевым фактором применения любой статистической модели является правильное понимание предметной области и ее бизнес-приложения.
Линейная регрессия — это довольно простой, но мощный инструмент, который может существенно облегчить работу аналитика при изучении поведения потребителей; факторов, влияющих на производительность и окупаемость; улучшит понимание бизнес процессов в целом.
Примеры использования линейной регрессии
Прогнозирование показателей
Данную модель можно использовать для обнаружения тенденций и составления прогнозов. Предположим, продажи компании росли на протяжении двух лет. Путем проведения линейного анализа данных о ежемесячных продажах компания могла бы спрогнозировать продажи в будущие месяцы.
Оценка эффективности маркетинга
Линейная регрессия также может использоваться для оценки эффективности маркетинга, рекламных кампаний и ценообразования. Чтобы компания «XYZ» оценила качественную отдачу от средств, потраченных на маркетинг определенного бренда, достаточно построить график линейной регрессии и посмотреть, как связаны затраты с прибылью.
Прелесть линейной регрессии в том, что она позволяет улавливать отдельные воздействия каждой маркетинговой кампании, а также контролировать факторы, которые могут повлиять на продажи.
В реальных сценариях обычно существует несколько рекламных кампаний, которые проводятся в один и тот же период времени. Предположим, что две кампании запускаются на телевидении и радио параллельно. Построенная модель может уловить как изолированное, так и комбинированное влияние одновременного показа этой рекламы.
Оценка риска
Модель линейной регрессии хорошо работает для расчета рисков в сфере финансов или страхования. К примеру, компания по страхованию автомобилей может построить линейную регрессию, чтобы составить таблицу выплат по страховке, используя отношение прогнозируемых исков к заявленной страховой стоимости. Основными факторами в такой ситуации являются характеристики автомобиля, данные о водителе или демографическая информация. Результаты такого анализа помогут в принятии важных деловых решений.
Обнаружение важных факторов
В индустрии кредитования финансовая компания заинтересована в минимизации рисков. Поэтому ей важно понять пять основных факторов, вызывающих неплатежеспособность клиента. На основе результатов регрессионного анализа компания могла бы выявить эти факторы и определить варианты EMI (Equated Monthly Installment – фиксированный платеж, произведенный заемщиком кредитору в течение оговоренного срока), чтобы минимизировать дефолт среди сомнительных клиентов.
Ценообразование активов
Еще модель линейной регрессии находит свое применение в ценообразовании активов. «Модель оценки долгосрочных активов» описывает связь между ожидаемой доходностью и риском инвестирования в ценную бумагу. Это помогает инвесторам оценивать целесообразность инвестиций и доходность их портфеля.
Вывод
Несмотря на то, что линейная регрессия имеет довольно жесткие ограничения, поскольку она может работать только тогда, когда зависимая переменная имеет непрерывный характер и имеется линейная зависимость между переменными, модель является самым известным методом анализа и прогнозирования.
Мы привели самые популярные примеры использования данной модели в бизнесе и финансах. Естественно, чтобы глубоко понять, как его использовать в той или иной ситуации, нужно погрузиться в метод поподробнее – самостоятельно «пощупать» все его слабые и сильные стороны; посмотреть, как модель ведет себя на уникальных данных и так далее. Это очень интересный и важный процесс – именно поэтому индустрия Data Science сейчас находится на таком подъеме!
Автор: Алексанян Андрон, эксперт SF Education