Облигации: оценка стоимости и рисков
 4 мин
4 мин
 2575
2575  10 Июн 2020
10 Июн 2020 
Основатель и Генеральный директор, SF Education

Облигация – долговая ценная бумага, по которой эмитент (организация, выпустившая облигацию) обязуется возвратить инвестору занятую у него сумму, а также выплачивать проценты в течение определенного времени. Владелец облигации заранее знает, когда и сколько получит процентов и основную сумму займа. Ниже представлены виды облигаций.
По форме выплаты дохода:
- Бескупонные – инвестор покупает облигацию по скидке, а в конце сроке получает номинальную стоимость. Проценты в виде купонов он не получает;
- Купонные – платят инвестору регулярные проценты, а в конце возмещают номинальную стоимость. Это классический вид облигаций (также называют vanilla bonds)
По форме погашения:
- Краткосрочные (до 1 года);
- Среднесрочные (от 1 года до 5 лет);
- Долгосрочные (от 5 лет).
По способу обращения:
- Со свободным обращением;
- С ограниченным обращением (например, владелец не может продавать облигацию в течение какого-то времени).
Приведенная стоимость облигации (справедливая цена) рассчитывается по формуле:
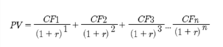
CF – денежный поток за период;
r – ставка дисконтирования;
n – порядковый номер периода
Нужно помнить, что справедливая стоимость облигации не будет всегда равно рыночной, так как инвестор может иметь иную требую норму доходности (ставку дисконтирования), чем рынок в целом. В таком случае инвестор не будет покупать облигацию.
Пример
- 5-летняя облигация;
- Ежегодные платежи (в конце года);
- Номинальная стоимость – 1000 рублей;
- Купонная ставка – 10%
- Требуемая доходность – 12%.
Чему равна ее стоимость сегодня?
Решение
Размер годового купона (денежного потока) равен 100 рублям [1000 рублей номинальная стоимость х 10% купонная ставка].
Вставляем значения из условия и расчетов выше в формулу:
PV = 100 / (1 + 12%) ^ 1 + 100 / (1 + 12%) ^ 2 +…+ 1100 / (1 + 12%) ^ 5 = 928 рублей
Заметьте, что, если требуемая доходность равна купонной ставке, ты рыночная стоимость облигации равна номинальной!
Пример
- 5-летняя облигация;
- Платежи два раза в год (в середине и в конце года)
- Номинальная стоимость – 1000 рублей;
- Купонная ставка – 10%
- Требуемая доходность – 12%.
Решение
Размер годового купона (денежного потока) равен 100 рублям [1000 рублей номинальная стоимость х 10% купонная ставка]. Размер одного купона равен 50 рублям (так как облигация платит купоны дважды в год).
Вставляем значения из условия и расчетов выше в формулу:
PV = 50 / (1 + 12% / 2) ^ 1 + 50 / (1 + 12% / 2) ^ 2 +…+ 1050 / (1 + 12% / 2) ^ 10 = 926 рублей
Значение текущей цены (приведенной стоимости) чуть ниже в этом примере, так как последний платеж (с возвратом первоначального вложения инвестору) составляет 1050 рублей (1000 рублей номинала плюс 50 рублей процентов), а не 1100 рублей, как в Примере 1.
При покупке облигации инвестор берет на себя два ключевых риска: кредитный — риск дефолта эмитента (ситуация, когда эмитент не может расплатиться по долгам), и процентный — риск колебаний рыночной стоимости бумаги в ответ на изменение уровня процентных ставок в экономике (по сути, риск того, что инвестор упустит доходность, если ставки вырастут, так как из-за роста процентных ставок в экономике облигация не начнет платить более высокие купоны).
Оценку кредитных рисков мы рассмотрим потом. Для оценки процентных рисков используется такой показатель как дюрация (Duration). Если коротко, то дюрация показывает, примерно на сколько процентов упадет стоимость облигации, если процентные ставки на рынке вырастут (и наоборот).
Рассчитывается дюрация следующим образом:
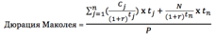
где: P — текущая цена облигации;
r — доходность к погашению;
t — период платежа (купона или номинала);
N — номинал облигации (в деньгах);
C — купонный платеж;
n — количество платежей.
Дюрация измеряется в годах. В этом нет ничего странного, потому что дюрация также показывает, за какой примерно срок инвестор «отбивает» половину инвестированной суммы в облигации (почитайте про канадского экономиста Фредерика Маколея, чтобы понять, как эта идея вообще появилась).
Пример 3
Компания А выпустила облигацию с номинальной стоимостью в 1000 рублей, которая платит купоны 1 раз в год в течение 5 лет. Купонная ставка – 7%. Рыночная ставка – 10%. Чему будет равна дюрация для этой облигации?
Решение
Размер купона составляет 70 рублей в год (7% х 1000 рублей). Текущая цена облигации (Р) рассчитывается как сумма дисконтированных денежных потоков (купонов), включая дисконтированную номинальную стоимость (то, что инвестор получит в конце срока). Таким образом получаем знаменатель: он равен 843 рублям.
Числитель выглядит более запутанным, но на самом деле он очень похож по расчетам на знаменатель. Например, для расчета второй части числителя мы берем номинал (1000 рублей), дисконтируем к сегодняшнему дню (степень 5, так как у нас пять лет до погашения) и умножаем получившееся значение на 5 (вес этого платежа по сравнению с другими платежами). Аналогично поступаем с каждым купоном, умножая на соответствующий вес и суммируя их. Так получаем числитель: он равен 3633 рублям.
В итоге получаем значение для дюрации – 4,31 (года) [3633 руб / 843 руб].
Таким образом, мы можем сказать, что, если процентные ставки на рынке вырастут на 1 процентный пункт (с 7% до 8%), то стоимость облигации упадет примерно на 4,31%.
Пример 4
Дюрация облигации равна 6,33 годам. Процентные ставки на рынке упали на 25 базисных пунктов (0,25%). Как изменится цена облигации?
Решение
Формула для расчета: (-значение дюрации) х (изменение в процентных ставках) = (-6.33) х (-0,25%) = 1,58%. Таким образом, если процентные ставки упадут на 25 базисных пунктов, облигация вырастет примерно на 1,6%.
Дюрация дает только приблизительную оценку процентных рисков и подходит лишь для небольших изменений доходности (рыночных ставок). Все дело в том, что зависимость цены облигации от ее доходности не линейная, а представляет из себя кривую (причем эта зависимость обратная: чем выше ожидаемая доходность – дисконтная ставка – тем ниже цена облигации).
Для того, чтобы снизить погрешность вычислений, используют еще один параметр, называющийся выпуклость кривой «Цена/Доходность».
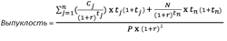
Чтобы не усложнять, предлагаем запомнить такое правило относительно выпуклости: выпуклость всегда «работает» на инвестора: если процентные ставки растут, то выпуклость уменьшает падение в цене облигации (то есть облигация падает в цене на меньшее значение, чем предсказывает ее дюрация), а если процентные ставки падают, то облигация растет в цене сильнее, чем предсказывает ее дюрация.
Ознакомиться с другими примерами расчета стоимости облигаций можно по ссылке.
Получить знания и навыки, необходимые для работы в финансовой сфере, можно на программе «Финансовая Академия» от SF Education!



